Chapter 2
Overcoming Mathophobia: Reading and Understanding Mathematical Expressions
IN THIS CHAPTER
 Reading mathematical notation
Reading mathematical notation
 Understanding formulas and what they mean
Understanding formulas and what they mean
 Working with arrays (collections of numbers)
Working with arrays (collections of numbers)
Let’s face it: Many people fear math, and statistical calculations require math. In this chapter, we help you become more comfortable with reading mathematical expressions, which are combinations of numbers, letters, math operations, punctuation, and grouping symbols. We also help you become more comfortable with equations, which connect two expressions with an equal sign. And we review formulas, which are equations designed for specific calculations. (For simplicity, for the rest of the chapter, we use the term formula to refer to expressions, equations, and formulas.) We also explain how to write formulas, which you need to know in order to tell a computer how to do calculations with your data.
We start the chapter by showing you how to interpret the mathematical formulas you encounter throughout this book. We don’t deconstruct the intricacies of complicated mathematical operations. Instead, we explain how mathematical operations are indicated in this book. If you feel unsure of your grasp on algebra, consider reviewing Algebra I For Dummies and Algebra II For Dummies, which are both written by Mary Jane Sterling and published by Wiley.
Breaking Down the Basics of Mathematical Formulas
One way to think of a mathematical formula is as a shorthand way to describe how to do a certain calculation. Formulas are made up of numbers, constants, and variables interspersed with symbols that indicate mathematical operations, punctuation, and typographic effects. Formulas are constructed using relatively standardized rules that have evolved over centuries. In the following sections, we describe two different kinds of formulas that you encounter in this book: typeset and plain text. We also describe two of the building blocks from which formulas are created: constants and variables.
Displaying formulas in different ways
Formulas can be expressed in print in two different formats: typeset format and plain text format:
- A typeset format utilizes special symbols, and when printed, the formula is spread out in a two-dimensional structure, like this:
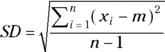
- A plain text format prints the formula out as a single line, which is easier to type if you’re limited to the characters on a keyboard:
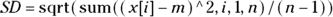
Checking out the building blocks of formulas
No matter how they’re written, formulas are essentially recipes that tell you how to calculate a result, or how a value is defined. To cook up your own result, you need to know how to follow the recipe. When initially approaching a formula, it’s helpful to start by examining the building blocks from which formulas are constructed. These include constants, which are numbers with specified values, and variables, which represent quantities that can take on different values at different times.
Constants
Constants are values that can be represented explicitly (using the numerals 0 through 9 with or without a decimal point), or symbolically (using a letter in the Greek or Roman alphabet). Symbolic constants represent a particular value important in mathematics, physics, or some other discipline, such as:
- The Greek letter π usually represents 3.14159 (plus a zillion more digits). This Greek letter is spelled pi and pronounced pie, and represents the ratio of the circumference of any circle to its diameter.
The number 2.71828 (plus a zillion more digits) is represented by e (which is italicized when written, and is pronounced like the letter “e”). Later in this chapter, we describe one way e is used. You’ll see e in statistical formulas throughout this book and in almost every other mathematical and statistical textbook. Whenever you see an italicized e in this book, it refers to the number 2.718 unless we explicitly say otherwise.
 The official mathematical definition of e is: The value of the expression
The official mathematical definition of e is: The value of the expression  , which approaches infinity as n gets larger and larger. Unlike π, e has no simple geometrical interpretation. Here is an example used to help learners envision e: Assume you put exactly one dollar in a bank account that’s paying 100 percent annual interest, compounded continuously. After exactly one year, your account will have e dollars in it. That includes the interest on your original dollar, plus the interest on the interest — about $1.72 (to the nearest penny) — added to the original dollar for a total of $2.72. (This is just an example. We don’t think there is a single bank out there advertising annual returns in terms of e!)
, which approaches infinity as n gets larger and larger. Unlike π, e has no simple geometrical interpretation. Here is an example used to help learners envision e: Assume you put exactly one dollar in a bank account that’s paying 100 percent annual interest, compounded continuously. After exactly one year, your account will have e dollars in it. That includes the interest on your original dollar, plus the interest on the interest — about $1.72 (to the nearest penny) — added to the original dollar for a total of $2.72. (This is just an example. We don’t think there is a single bank out there advertising annual returns in terms of e!)
Mathematicians and scientists use lots of other specific Greek and Roman letters as symbols for specific constants, but you need only a few of them in your biostatistics work. π and e are the most common, and we define others in this book as they come up in topics we present.
Variables
The term variable has two slightly different meanings:
- In mathematics and engineering, a variable is a symbol that represents some quantity in a formula. It is usually a letter of the alphabet. You are probably used to seeing variables like x and y in algebra, for example.
- In statistics and computer science, a variable is a name referring to a single data value or an entire field, which is a column of data in a spreadsheet or database. The variable name is made up of letters (like SBP for systolic blood pressure), but may also contain numbers (such as SBP1, SBP2, and SBP3). Technically, the variable name refers to a place in the computer’s memory where the data value or field is stored. For example, a computer programmer writing a statistical software program may ask if the variable SBP is greater than or equal to 120 mmHg.
The names of variables may be written in uppercase or lowercase letters depending upon typographic conventions or preferences, or on the requirements of the software being used.
Focusing on Operations Found in Formulas
A formula tells you how the building blocks of numbers, constants, and variables are to be combined. In other words, a formula is a recipe for the calculations you’re supposed to carry out on these quantities. But formulas are not always easy to read. A particular symbol — such as the minus sign — can be interpreted differently, depending upon the context of the formula. Also, a particular mathematical operation like multiplication can be represented in different ways in a formula. In the following sections we explain the basic mathematical operations you see in formulas throughout this book and describe two types of equations you’ll encounter in statistical books and articles.
Basic mathematical operations
The four basic mathematical operations are addition, subtraction, multiplication, and division (ah, yes — the basics you learned in elementary school). Different symbols are associated with these operations, as you discover in the following sections.
Addition and subtraction
Addition and subtraction are always indicated by the + and – symbols, respectively, placed between two numbers or variables. Compared to the plus sign, the minus sign can be tricky when it comes to interpreting it in a formula.
- A minus sign placed immediately before a number indicates a negative quantity. For example, –5° indicates five degrees below 0, and –5 kg indicates a weight loss of 5 kilograms.
- A minus sign placed immediately before a variable tells you to reverse the sign of the value of the variable. Therefore, –x means that if x is positive, you should now make it negative. But it also means that if x is negative, make it positive (so, if x was –5 kg, then –x would be 5 kg). Used this way, the minus sign is referred to as a unary operator because it’s acting on only one variable.
Multiplication
The word term is generic for an individual item or element in a formula. Multiplication of terms is indicated in several ways, as shown in Table 2-1.
TABLE 2-1 Multiplication Options
What It Is |
Example |
Where It’s Used |
|---|---|---|
Asterisk |
|
Plain text formulas, but almost never in typeset formulas |
Cross |
|
Typeset formula, between two variables or two constants being multiplied together |
Raised dot |
|
Typeset formula |
Term is immediately in front of a parenthesized expression |
|
Typeset formula |
Brackets and curly braces |
|
Typeset formula containing “nested” parentheses |
Two or more terms running together |
|
In typeset formulas only |
Division
Like multiplication, division can be indicated in several ways:
- With a slash (/) in plain text formulas: Distance/Time
- With a division symbol (÷) in typeset formulas: Distance ÷ Time
- With a long horizontal bar in typeset formulas:

Powers, roots, and logarithms
In the next section, we cover powers, roots, and logarithms, all three of which are related to the idea of repeated multiplication.
Raising to a power
Raising to a power is a shorthand way to indicate repeated multiplication by the same number. You indicate raising to a power by:
- Superscripting in typographic formulas, such as
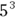
- Using ** in plain text formulas, such as
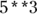
- Using ^ in plain text formulas, such as
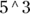
All the preceding expressions are read as “five to the third power,” “five to the power of three,” or “five cubed.” It says to multiply three fives together: 5 × 5 × 5, which gives you 125.
Here are some other features of power:
- A power doesn’t have to be a whole number. You can raise a number to a fractional power (such as 3.8). You can’t visualize this in terms of repeated multiplications, but your scientific calculator can show you that
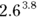 is equal to approximately 37.748.
is equal to approximately 37.748. - A power can be negative. A negative power indicates the reciprocal of the quantity, which is when you divide the quantity by 1 (meaning
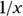 ). So
). So 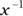 means 1 divided by x, and in general,
means 1 divided by x, and in general, 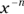 is the same as
is the same as  (such as 2–3 = ½).
(such as 2–3 = ½).
Remember the constant e (2.718…)? Almost every time you see e used in a formula, it’s being raised to some power. This means you almost always see e with an exponent after it. Raising e to a power is called exponentiating, and another way of representing 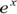 in plain text is exp(x). Remember, x doesn’t have to be a whole number. By typing =exp(1.6) in the formula bar in Microsoft Excel (or doing the equation on a scientific calculator), you see that exp(1.6) equals approximately 4.953. We talk more about exponentiating in other book sections, especially Chapters 18 and 24.
in plain text is exp(x). Remember, x doesn’t have to be a whole number. By typing =exp(1.6) in the formula bar in Microsoft Excel (or doing the equation on a scientific calculator), you see that exp(1.6) equals approximately 4.953. We talk more about exponentiating in other book sections, especially Chapters 18 and 24.
Taking a root
Taking a root involves asking the power question backwards. In other words, we ask: “What base number, when raised to a certain power, equals a certain number?” For example, “What number, when raised to the power of 2 (which is squared), equals 100?” Well, 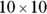 (also expressed
(also expressed  ) equals 100, so the square root of 100 is 10. Similarly, the cube root of 1,000,000 is 100, because
) equals 100, so the square root of 100 is 10. Similarly, the cube root of 1,000,000 is 100, because  (also expressed
(also expressed 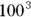 ) equals a million.
) equals a million.
Root-taking is indicated by a radical sign (√) in a typeset formula, where the term from which we intend to take the root is located “under the roof” of the radical sign, as 25 is shown here: 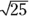 . If no numbers appear in the notch of the radical sign, it is assumed we are taking a square root. Other roots are indicated by putting a number in the notch of the radical sign. Because
. If no numbers appear in the notch of the radical sign, it is assumed we are taking a square root. Other roots are indicated by putting a number in the notch of the radical sign. Because  is 256, we say 2 is the eighth root of 256, and we put 8 in the notch of the radical sign covering 256, like this:
is 256, we say 2 is the eighth root of 256, and we put 8 in the notch of the radical sign covering 256, like this:  . You also can indicate root-taking by expressing it different ways used in algebra:
. You also can indicate root-taking by expressing it different ways used in algebra: 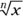 is equal to
is equal to 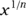 and can be expressed as
and can be expressed as 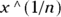 in plain text.
in plain text.
Looking at logarithms
In addition to root-taking, another way of asking the power question backwards is by saying, “What exponent (or power) must I raise a particular base number to in order for it to equal a certain number?” For root-taking, in terms of using a formula, we specify the power and request the base. With logarithms, we specify the base and request the power (or exponent).
For example, you may ask, “What power must I raise 10 to in order to get 1,000?” The answer is 3, because 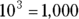 . You can say that 3 is the logarithm of 1,000 (for base 10), or, in mathematical terms:
. You can say that 3 is the logarithm of 1,000 (for base 10), or, in mathematical terms: 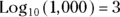 . Similarly, because
. Similarly, because 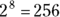 , you say that
, you say that  . And because
. And because 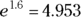 , then
, then 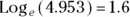 .
.
There can be logarithms to any base, but three bases occur frequently enough to have their own nicknames:
- Base-10 logarithms are called common logarithms.
- Base-e logarithms are called natural logarithms.
- Base-2 logarithms are called binary logarithms.
An antilogarithm (usually shortened to antilog) is the inverse of a logarithm. As an example of an antilog, if y is the log of x, then x is the antilog of y. For another example, the base-10 logarithm of 1,000 is 3, so the base-10 antilog of 3 is 1,000.
Factorials and absolute values
So far we’ve covered mathematical operators that are written either between the two numbers, which are the subject of the operation (such as the plus in 5 + 8), or before the number it operates on if there is only one number (like the minus sign used as a unary operator described earlier, as in –5°). Next we cover factorials and absolute values, which are mathematical operators that have a unique format in typeset expressions.
Factorials
Although a statistical formula may contain an exclamation point, that doesn’t mean that you should sound excited when you read the formula aloud (although it may be tempting to do so!). An exclamation mark (!) after a number is shorthand for calculating that number’s factorial. To do that, you write down all the whole numbers from 1 to the factorial number in a row, and then multiply them all together. For example, the expression 5!, which is read as five factorial, means to calculate  (which equals 120).
(which equals 120).
Even though standard keyboards have a ! key, most computer programs and spreadsheets don’t let you use ! to indicate factorials. For example, to do the calculation of 5! in Microsoft Excel, you use the formula =FACT(5).
- Factorials can be very large. For example, 10! is 3,628,800, and 170! is about
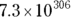 , which is close to the processing limits for many computers.
, which is close to the processing limits for many computers. - 0! isn’t 0, but is actually 1. Actually, it’s the same as 1!, which is also 1. That may not make obvious sense, but is true, so you can memorize it.
- The definition of factorial can be extended to fractions and even to negative numbers. But good news! You don’t have to deal with those kinds of factorials in this book.
Absolute values
The term absolute value refers to the value of a number when it is positive (meaning it has no minus sign before it). You indicate absolute value by placing vertical bars immediately to the left and right of the number. So |5.7| equals 5.7, and |–5.7| also equals 5.7. Even though most keyboards have the | (pipe) symbol, the absolute value is usually indicated in plain text formulas as abs(5.7).
Functions
In this book, a function is a set of calculations that accepts one or more numeric values (called arguments) and produces a numeric result. Regardless of typeset or plain text, a function is indicated in a formula by the function name followed by a set of parentheses that contain the argument or arguments. Here’s an example of the function square root of x: sqrt(x).
The most commonly used functions have been given standard names. The preceding sections in this chapter covered some of these, including sqrt for square root, exp for exponentiate, log for logarithm, ln for natural log, fact for factorial, and abs for absolute value.
Simple and complicated formulas
Simple formulas have one or two numbers and only one mathematical operator (for example, 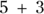 ). But most statistical formulas you’ll encounter are more complicated, with two or more operators and variables.
). But most statistical formulas you’ll encounter are more complicated, with two or more operators and variables.
- Evaluate any terms and operations within parentheses, brackets, curly braces, or absolute-value bars first, including terms inside parentheses that follow the name of a function. Please note that nested functions are evaluated inside out, so additional parentheses may be needed to prevent any confusion.
- Evaluate negation, factorials, powers, and roots.
- Evaluate multiplication and division.
- Evaluate addition and subtraction.
Equations
An equation has two expressions with an equal sign between them. Most equations appearing in this book have a single variable name to the left of the equal sign and a formula to the right, like this: 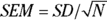 . This style of equation defines the variable appearing on the left in terms of the calculations specified on the right. In doing so, it also provides the “cookbook” instructions for calculating the result, which in this case is the SEM for any values of SD and N.
. This style of equation defines the variable appearing on the left in terms of the calculations specified on the right. In doing so, it also provides the “cookbook” instructions for calculating the result, which in this case is the SEM for any values of SD and N.
The book also contains another type of equation that appears in algebra, asserting that the terms on the left side of the equation are equal to the terms on the right. For example, the equation 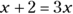 asserts that x is a number that, when added to 2, produces a number that’s 3 times as large as the original x. Algebra teaches you how to solve this expression for x, and it turns out that the answer is
asserts that x is a number that, when added to 2, produces a number that’s 3 times as large as the original x. Algebra teaches you how to solve this expression for x, and it turns out that the answer is 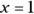 .
.
Counting on Collections of Numbers
A variable can refer to one value or to a collection of values called arrays. Arrays can come with one or more dimensions.
One-dimensional arrays
A one-dimensional array can be thought of as a list of values. For instance, you may record a list of fasting glucose values (in milligrams per deciliter, 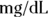 ) from five study participants as 86, 110, 95, 125, and 64. You could use the variable name Gluc to refer to this array containing five numbers, or elements. Using the term Gluc in a formula refers to the entire five-element array.
) from five study participants as 86, 110, 95, 125, and 64. You could use the variable name Gluc to refer to this array containing five numbers, or elements. Using the term Gluc in a formula refers to the entire five-element array.
You can refer to one particular element of this array (meaning one glucose measurement) in several ways. You can use the index of the array, which is the number that indicates the position of the element to which you are referring in the array.
- In a typeset formula, indices are typically indicated using subscripts. For example,
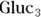 refers to the third element in the array (which would be 95 in our example).
refers to the third element in the array (which would be 95 in our example). - In a plain text formula, indices are typically indicated using brackets (such as Gluc[3]).
The index can be a variable like I, so Gluc[i] would refer to the ith element of the array. The term ith means the variable would be allowed to take on any value between 1 and the maximum number of elements in the array (which in this case would be 5).
Higher-dimensional arrays
Two-dimensional arrays can be understood as a table of values with rows and columns, like a block of cells in a spreadsheet. There are also higher-dimensional arrays that can be thought of as a whole collection of tables. Suppose that you measure the fasting glucose on five participants on each of three treatment days. You could think of your 15 measurements being laid out in a table with five rows and three columns. If you want to represent this entire table with a single variable name like Gluc, you can use double-indexing, with the first index specifying the participant (1 through 5), and the second index specifying the day of the measurement (1 through 3). Under that system, Gluc[3,2] indicates the fasting glucose measurement for participant 3 on day 2. To express the array as a formula, we would use the expression Gluc[i,j], which specifies the fasting glucose for the ith subject on the jth day.
- A one-dimensional array is also referred to as a vector. But this can be confusing, because the term vector is also used in mathematics, physics, and biology to refer to completely different concepts.
- A two-dimensional array is sometimes called a matrix (plural: matrices). To some, this term implies we are using a set of mathematical rules called matrix algebra, and that’s not entirely incorrect. Mathematical descriptions of multiple regression (covered in Chapter 17 of this book) make extensive use of matrix algebra. Also, computer software may refer to tabular objects with the term matrix.
Arrays in formulas
If you see an array name in a formula without any subscripts, it usually means that you have to evaluate the formula for each element of the array, and the result is an array with the same number of elements. So, if Gluc refers to the array with the five elements 86, 110, 95, 125, and 64, then the expression 2 × Gluc results in an array with each element in the same order multiplied by two: 172, 220, 190, 250, and 128.
When an array name appears in a formula with subscripts, the meaning depends upon the context. It can indicate that the formula is to be evaluated only for some elements of the array, or it can mean that the elements of the array are to be combined in some way before being used (as described in the next section).
Sums and products of the elements of an array
This Greek letter ∑ is known in English as capital sigma. Though harmless, ∑ strikes terror into the hearts of many learners as they encounter it statistics books and articles (not to mention its less common but even scarier cousin Π, also known as capital pi). Uppercase sigma and pi — namely ∑ and Π — correspond to the Roman letters S and P, which stand for Sum and Product, respectively. These symbols are almost always used in front of variables and expressions that represent arrays.
When you see ∑ in a formula, just think of it as saying “sum of.” Assuming an array named Gluc that is comprised of the five elements 86, 110, 95, 125, and 64, you can read the expression 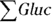 as “the sum of the Gluc array” or “sum of Gluc.” To evaluate it, add all five elements together to get
as “the sum of the Gluc array” or “sum of Gluc.” To evaluate it, add all five elements together to get 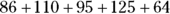 , which equals 480.
, which equals 480.
Sometimes the ∑ notation is written in a more complex form, where the index variable i is displayed under (or to the right of) the ∑ as a subscript of the array name, like this: 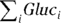 . Though its meaning is the same as
. Though its meaning is the same as 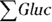 , you would read it as, “the sum of the Gluc array over all values of the index i” (which produces the same result as
, you would read it as, “the sum of the Gluc array over all values of the index i” (which produces the same result as 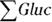 , which is 480). The subscripted ∑ form is helpful in expressing multi-dimensional arrays, when you may want to sum over only one of the dimensions. For example, if Ai,j is a two-dimensional array:
, which is 480). The subscripted ∑ form is helpful in expressing multi-dimensional arrays, when you may want to sum over only one of the dimensions. For example, if Ai,j is a two-dimensional array:
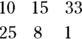
then 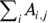 means that you should sum over the rows (the i subscript) to get the one-dimensional array: 35, 23, and 34. Likewise,
means that you should sum over the rows (the i subscript) to get the one-dimensional array: 35, 23, and 34. Likewise, 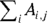 means to sum across the columns (j’) to get the one-dimensional array: 58, 34.
means to sum across the columns (j’) to get the one-dimensional array: 58, 34.
Finally, you may see the full-blown official mathematical ∑ in all its glory, like this:
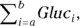
which reads “sum of the Gluc array over values of the index i going from a to b, inclusive.” So if a was equal to 1, and b was equal to 5, the expression would become:
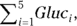
which is just another way of summing all the elements, producing 480. But if you wanted to omit the first and last elements of the array from the sum, you could write:
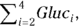
This expression says to add up only Gluc2 + Gluc3 + Gluc4, to get 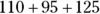 , which would equal 330.
, which would equal 330.
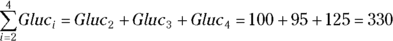
Π works just like ∑, except that you multiply instead of add:

 You must know how to read both types of formula displays — typeset and plain text. The examples in this chapter show both styles. But you may never have to construct a professional-looking typeset formula (unless you’re writing a book, like we’re doing right now). On the other hand, you’ll almost certainly have to write out plain text formulas as part of organizing, preparing, editing, and analyzing your data.
You must know how to read both types of formula displays — typeset and plain text. The examples in this chapter show both styles. But you may never have to construct a professional-looking typeset formula (unless you’re writing a book, like we’re doing right now). On the other hand, you’ll almost certainly have to write out plain text formulas as part of organizing, preparing, editing, and analyzing your data.
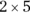
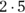
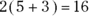
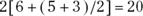

 You can put terms right next to each other to imply multiplication only when it’s perfectly clear from the context of the formula that the authors are using only single-letter variable names (like x and y), and that they’re describing calculations where it makes sense to multiply those variables together. In other words, you can’t put numeric terms right after one another to imply multiplication, meaning you can’t replace 5 × 3 with 53, because 53 is an actual number itself. And you shouldn’t replace variables like length × width with lengthwidth, because it looks like you’re referring to a single variable named lengthwidth.
You can put terms right next to each other to imply multiplication only when it’s perfectly clear from the context of the formula that the authors are using only single-letter variable names (like x and y), and that they’re describing calculations where it makes sense to multiply those variables together. In other words, you can’t put numeric terms right after one another to imply multiplication, meaning you can’t replace 5 × 3 with 53, because 53 is an actual number itself. And you shouldn’t replace variables like length × width with lengthwidth, because it looks like you’re referring to a single variable named lengthwidth.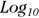 , and when referring to binary logarithms, we use
, and when referring to binary logarithms, we use 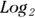 .
.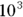 , or 1,000). Similarly, the natural antilog of any number is e (2.718) raised to the power of that number. As an example, the natural antilog of 5 is
, or 1,000). Similarly, the natural antilog of any number is e (2.718) raised to the power of that number. As an example, the natural antilog of 5 is 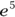 , or approximately 148.41.
, or approximately 148.41. In a typeset fraction, evaluate terms and operations above the horizontal bar (the numerator) first, then terms and operations below the bar (the denominator) next. After that, divide the numerator by the denominator.
In a typeset fraction, evaluate terms and operations above the horizontal bar (the numerator) first, then terms and operations below the bar (the denominator) next. After that, divide the numerator by the denominator.