Chapter 11
Comparing Average Values between Groups
IN THIS CHAPTER
 Determining which tests should be used in different situations
Determining which tests should be used in different situations
 Preparing your data, running tests, and interpreting the output
Preparing your data, running tests, and interpreting the output
 Estimating the sample size you need to compare average values
Estimating the sample size you need to compare average values
Comparing average values between groups of numbers is part of almost all biostatistical analyses, and over the years, statisticians have developed dozens of tests for this purpose. These tests include several different flavors of the Student t test, analyses of variance (ANOVA), and a dizzying collection of tests named after the men who popularized them, including Welch, Wilcoxon, Mann-Whitney, and Kruskal-Wallis, to name just a few. The multitude of tests is enough to make your head spin, which leaves many researchers with the uneasy feeling that they may be using the wrong statistical test on their data.
In this chapter, we guide you through the menagerie of statistical tests for comparing groups of numbers. We start by explaining why there are so many tests available, then guide you as to which ones are right for which situations. Next, we show you how to execute these tests using R software, and how to interpret the output. We focus on tests that are usually provided by modern statistical programs (like those discussed in Chapter 4, which also explains how to install and get started with R).
Grasping Why Different Situations Need Different Tests
You may wonder why there are so many tests for such a simple task as comparing averages. Well, “comparing averages” doesn’t refer to a specific situation. It’s a broad term that can apply to different situations where you are trying to compare averages. These situations can differ from each other on the basis of these and other factors, which are listed here in order of most to least common:
- Within or between: You could be testing differences within groups or differences between groups.
- Number of time points: You could be testing differences occurring at one point or over a number of time points.
- Number of groups: You could be testing differences between two groups or between three or more groups.
- Distribution of outcome: Your outcome measurement could follow the normal distribution or some other distribution (see Chapter 3).
- Variation: You could be testing the differences in variation or spread across groups (see Chapter 3).
These different factors can occur in any and all combinations, so there are a lot of potential scenarios. In the following sections, we review situations you may frequently encounter when analyzing biological data, and advise you as to how to select the most appropriate testing approach given the situation.
Comparing the mean of a group of numbers to a hypothesized value
Sometimes you have a measurement from the literature (called a historical control) that provides a hypothesized value of your measurement, and you want to statistically compare the average of a group to this mean. This situation is common when you are comparing a value that was calculated based on statistical norms derived based on the population (such as the IQ test, where 100 has been scaled to be the population mean).
Typically, comparing a group mean to a historical control warrants using the one-group Student t test that we describe in the later section “Surveying Student t tests.” For data that are not normally distributed, the Wilcoxon Signed-Ranks (WSR) test can be used instead, although it is not used often so we do not cover it in this chapter. (If you need a review on what normally distributed means, see Chapter 3.)
Comparing the mean of two groups of numbers
Comparing the mean of two groups of numbers is probably the most common situation encountered in biostatistics. You may be comparing mean levels of a protein that is a hypothesized disease biomarker between a group of patients known to have the disease and a group of healthy controls. Or, you may be comparing a measurement of drug efficacy between two groups of patients with the same condition who are taking two different drugs. Or, you may be comparing measurements of breast cancer treatment efficacy in women on one health insurance plan compared to those on another health insurance plan.
- The values must be normally distributed (called the normality assumption). For data that are not normally distributed, instead of the t-test, you can use the nonparametric Wilcoxon Sum-of-Ranks test (also called the Mann-Whitney U test and the Mann-Whitney test). We demonstrate the Wilcoxon Sum-of-Ranks test later in this chapter in the section “Running nonparametric tests.”
- The standard deviation (SD) of the values must be close for both groups (called the equal variance assumption). As a reminder, the SD is the square root of the variance. To remember why accounting for variation is important in sampling, review Chapter 3. Also, Chapter 9 provides more information about the importance of SD. If the two groups you are comparing have very different SDs, you should not use a Student t test, because it may not give reliable results, especially if you are also comparing groups of different sizes. A rule of thumb is that one group’s SD divided by another group’s SD should not be more than 1.5 to quality for a Student t test. If you feel your data do not qualify, you can use an alternative called the Welch test (also called the Welch t test, or the unequal-variance t test). As you see later in this chapter under “Surveying Student t tests,” because the Welch test accounts for both equal and unequal variance, it is the only one that is included in R statistical software.
Comparing the means of three or more groups of numbers
Comparing the means of three or more groups of numbers is an obvious extension of the two-group comparison in the preceding section. For example, you may have recorded some biological measurement, like a value indicating level of response to treatment among three diagnostic groups (such as mild, moderate, and severe periodontitis). A comparison of the means of three or more groups is handled by the analysis of variance (ANOVA), which we describe later in this chapter under “Assessing the ANOVA.” When there is one grouping variable, like severity of periodontitis, you have a one-way ANOVA. If the grouping variable has three levels (like mild, moderate, and severe periodontitis), it’s called a one-way, three-level ANOVA.
The null hypothesis of the one-way ANOVA is that all the groups have the same mean. The alternative hypothesis is that at least one group has a mean that is statistically significantly different from at least one of the other groups. The ANOVA produces a single p value, and if that p is less than your chosen criterion (typically α = 0.05), you conclude that at least one of the means must be statistically significantly different from at least one of the other means. (For a refresher on hypothesis testing and p values, see Chapter 3.) But the problem with ANOVA is that if it is statistically significant, it doesn’t tell you which groups have means that are statistically significantly different. If you have a statistically significant ANOVA, you have to follow-up with one or more so-called post-hoc tests (described later under “Assessing the ANOVA”), which test for differences between the means of each pair of groups in your ANOVA.
You can also use the ANOVA to compare just two groups. However, this one-way, two-level ANOVA produces exactly the same p value as the classic unpaired equal-variance Student t test.
Comparing means in data grouped on several different variables
The ANOVA is a very flexible method in that it can accommodate comparing means across several grouping variables at once. As an example, you could use an ANOVA for comparing treatment response among participants with different levels of the condition (such as mild, moderate, and severe periodontitis), who come from different clinics (such as Clinic A and Clinic B), and have undergone different treatment approaches (such as using mouthwash or not). An ANOVA involving three different grouping variables is called a three-way ANOVA (and compares at a more granular level).
Like the t test, the ANOVA also assumes that the value you are comparing follows a normal distribution, and that the SDs of the groups you are comparing are similar. If your data are not normally distributed, you can use the nonparametric Kruskal-Wallis test instead of the one-way ANOVA, which we demonstrate later in the section “Running nonparametric tests.”
Adjusting for a confounding variable when comparing means
Sometimes you are aware the variable you are comparing, such as reduction in blood pressure, is influenced by not only a treatment approach (such as drug A compared to drug B), but also by other confounding variables (such as age, whether the patient has diabetes, whether the patient smokes tobacco, and so on). These confounders are considered nuisance variables because they have a known impact on the outcome, and may be more prevalent in some groups than others. If a large proportion of the group on drug A were over age 65, and only a small proportion of those on drug B were over age 65, older age would have an influence on the outcome that would not be attributable to the drug. Such a situation would be confounded by age. (See Chapter 20 for a comprehensive review of confounding.)
When you are comparing means between groups, you are doing a bivariate comparison, meaning you are only involving two variables: the group variable and the outcome. Adjusting for confounding must be done through a multivariate analysis using regression.
Comparing means from sets of matched numbers
Often when biostatisticians consider comparing means between two or more groups, they are thinking of independent samples of data. When dealing with study participants, independent samples means that the data you are comparing come from different groups of participants who are not connected to each other statistically or literally. But in some scenarios, your intention is to compare means from matched data, meaning some sort of pairing exists in the data. Here are some common examples of matched data:
- The values come from the same participants, but at two or more different times, such as before and after some kind of treatment, intervention, or event.
- The values come from a crossover clinical trial, in which the same participant receives two or more treatments at two or more consecutive phases of the trial.
- The values come from two or more different participants who have been paired, or matched, in some way as part of the study design. For example, in a study of participants who have Alzheimer’s disease compared to healthy participants, investigators may choose to age-match each Alzheimer’s patient to a healthy control when they recruit so both groups have the same age distribution.
Comparing means of matched pairs
If you have paired data, you must use a paired comparison. Paired comparisons are usually handled by the paired student t test that we describe later in this chapter under “Surveying Student t tests.” If your data aren’t normally distributed, you can use the nonparametric Wilcoxon Signed-Ranks test instead.
Using Statistical Tests for Comparing Averages
Now that you have reviewed the different types of comparisons, you can continue to consider the basic concepts behind them as you dig more deeply. In this section, we discuss executing these tests in statistical software and interpreting the output. We do that with several tests, including Student t tests, the ANOVA, and nonparametric tests.
Surveying Student t tests
In this section, we present the general approach to conducting a Student t test. We walk through the computational steps common to the different kinds of t tests, including one-group, paired, and independent. As we do that, we explain the computational differences between the different test types. Finally, we demonstrate how to run the t tests using open source software R, and explain how to interpret the output (see Chapter 4 for more information about getting started with R).
Understanding the general approach to a t test
- Calculate the difference (D) between the mean values you are comparing.
Calculate the precision of the difference, which is the magnitude of the random fluctuations in that difference.
For the t test, calculate the standard error (SE) of that difference (see Chapter 10 for a refresher on SE).
Calculate the test statistic, which in this case is t.
The test statistic expresses the size of the D relative to the size of its SE. That is:
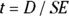 .
.Calculate the degrees of freedom (df) of the t statistic.
df is a tricky concept, but is easy to calculate. For t, the df is the total number of observations minus the number of means you calculated from those observations.
Use the t and df to calculate the p value.
The p value is the probability that random fluctuations alone could produce a t value at least as large as the value you just calculated based upon the Student t distribution.
The Student t statistic is always calculated using the general equation D/SE. Each specific type of t test we discussed earlier — including one-group, paired, unpaired, and Welch — calculates D, SE, and df slightly differently. These different calculations are summarized in Table 11-1.
TABLE 11-1 How t Tests Calculate Difference, Standard Error, and Degrees of Freedom
One-Group |
Paired |
Unpaired t Equal Variance |
Welch t Unequal Variance |
|
|---|---|---|---|---|
D |
Difference between mean of observations and a hypothesized value (h) |
Mean of paired differences |
Difference between means of the two groups |
Difference between means of the two groups |
SE |
SE of the observations |
SE of paired differences |
SE of difference, based on a pooled estimate of SD within each group |
SE of difference, from SE of each mean, by propagation of errors |
df |
Number of observations – 1 |
Number of pairs – 1 |
Total number of observations – 2 |
“Effective” df, based on the size and SD of the two groups |
Executing a t test
- For the one-group t test, you need the column of data containing the variable whose mean you want to compare to the hypothesized value (H), and you need to know H. R and other software enable you to specify a value for H and assumes 0 if you don’t specify anything. In the NHANES data, the fasting glucose variable is LBXGLU, so the R code to test the mean fasting glucose against a maximum healthy level of 100 mg/dL in an R dataframe named GLUCOSE is t.test(GLUCOSE$LBXGLU, mu = 100).
- For the paired t test, you need two columns of data representing the pair of numbers you want to enter into the paired t test. For example, in NHANES, systolic blood pressure (SBP) was measured in the same participant twice (variables BPXOSY1 and BPXOSY2). To compare these with a paired t test in an R dataframe named BP, the code is t.test(BP$BPXOSY1, BP$BPXOSY2, paired = TRUE).
- For the independent t test, you need to have one column coded as the grouping variable (preferable with a two-state flag coded as 0 and 1), and another column with the value you want to test. We created a two-state flag in the NHANES data called MARRIED where 1 = married and 0 = all other marital statuses. To compare mean fasting glucose level between these two groups in a dataframe named NHANES, we used this code: t.test(NHANES$LBXGLU ~ NHANES$MARRIED).
Interpreting the output from a t test
Listing 11-1 is the output from a one-sample t-test, where we tested the mean fasting glucose in the NHANES participants against the hypothesized mean of 100 mg/dL:
LISTING 11-1 R Output from a One-Sample Student t Test
> t.test(GLUCOSE$LBXGLU, mu = 100)
One Sample t-test
data: GLUCOSE$LBXGLU
t = 21.209, df = 4743, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
110.1485 112.2158
sample estimates:
mean of x
111.1821
The R output starts by stating what test was run and what data were used, and then reports the t statistic (21.209), the df (4743), and the p value, which is written in scientific notation: < 2.2e–16. If you have trouble interpreting this notation, just remove the < and then copy and paste the rest of the number into a cell in Microsoft Excel. If you do that, you will see in the formula bar that the number resolves to 0.00000000000000022 — which is a very low p value! The shorthand used for this in biostatistics is p < 0.0001, meaning it is sufficiently small. Because of this small p value, we reject the null hypothesis and say that the mean glucose of NHANES participants is statistically significantly different from 100 mg/dL.
But in what direction? For that, it is necessary to read down further in the R output, under 95 percent confidence interval. It says the interval is 110.1485 mg/dL to 112.2158 mg/dL (if you need a refresher on confidence intervals, read Chapter 10). Because the entire interval is greater than 100 mg/dL, you can conclude that the NHANES mean is statistically significantly greater than 100 mg/dL.
Now, let’s examine the output from the paired t test of SBP measured two times in the same participant, which is shown in Listing 11-2.
LISTING 11-2 R Output from a Paired Student t Test
> t.test(BP$BPXOSY1, BP$BPXOSY2, paired = TRUE)
Paired t-test
data: BP$BPXOSY1 and BP$BPXOSY2
t = 4.3065, df = 10325, p-value = 1.674e–05
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
0.1444651 0.3858467
sample estimates:
mean difference
0.2651559
Notice a difference between the output shown in Listings 11-1 and 11-2. In Listing 11-1, the third line of output says, “alternative hypothesis: true mean is not equal to 100.” That is because we specified the null hypothesis of 100 when we coded the one-sample t test. Because we did a paired t test in Listing 11-2, this null hypothesis now concerns 0 because we are trying to see if there is a statistically significant difference between the first SBP reading and the second in the same individuals. Why should they be very different at all? In Listing 11-2, the p value is listed as 1.674e–05, which resolves to 0.00001674 (to be stated as p < 0.0001). We were surprised to see a statistically significant difference! The output says that the 95 percent confidence interval of the difference is 0.1444651 mmHg to 0.3858467 mmHg, so this small difference may be statistically significant while not being clinically significant.
Let’s examine the output from our independent t test of mean fasting glucose values in NHANES participants who were married compared to participants with all other marital statuses. This output is shown in Listing 11-3.
LISTING 11-3 R Output from an Independent t Test
> t.test(NHANES$LBXGLU ~ NHANES$MARRIED)
Welch Two Sample t-test
data: NHANES$LBXGLU BY NHANES$MARRIED
t = –4.595, df = 4731.2, p-value = 4.439e–06
alternative hypothesis: true difference in means between group $
95 percent confidence interval:
–6.900665 –2.773287
sample estimates:
mean in group 0 mean in group 1
108.8034 113.6404
Importantly, at the top of Listing 11-3, notice that it says “Welch Two Sample t-test.” This is because R insists on using Welch’s test instead of the Student t test for independent t tests because Welch’s test accounts for unequal variance (as well as equal variance) between groups, as discussed earlier. In the output under the alternative hypothesis, notice that it says R is testing whether the true difference in means between group 0 and group 1 is not equal to 0 (remember, 1 = married and 0 = all other marital statuses). R calculated a p value of 4.439e–06, which resolves to 0.000004439 — definitely p < 0.0001! The groups are definitely statistically significantly different when it comes to average fasting glucose.
But which group is higher? Well, for that, you can look at the last line of the output, where it says that the mean in group 0 (all marital statuses except married) is 108.8034 mg/dL, and the mean in group 1 (married) is 113.6404 mg/dL. So does getting married raise your fasting glucose? Before you try to answer that, please make sure you read up on confounding in Chapter 20!
But what if you just wanted to know if the variance in the fasting glucose measurement in the married group was equal or unequal to the other group, even though you were doing a Welch test that accommodates both? For that, you can do an F test. Because we are not sure which group’s fasting glucose would be higher, we choose a two-sided F test and use this code: var.test(LBXGLU ~ MARRIED, NHANES, alternative = "two.sided"), which produces the output shown in Listing 11-4.
LISTING 11-4 R Output from an F Test
> var.test(LBXGLU ~ MARRIED, NHANES, alternative = "two.sided")
F test to compare two variances
data: LBXGLU by MARRIED
F = 0.97066, num df = 2410, denom df = 2332, p-value = 0.4684
alternative hypothesis: true ratio of variances is not equal to$
95 percent confidence interval:
0.8955321 1.0520382
sample estimates:
ratio of variances
0.9706621
As shown in Listing 11-4, the p value on the F test is 0.4684. As a rule of thumb:
- If
 , you would assume equal variances.
, you would assume equal variances. - If
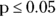 , you would assume unequal variances.
, you would assume unequal variances.
In this case, because the p value is greater than 0.05, equal variances can be assumed, and these data would qualify for the classic Student t test. As described earlier, R gets around this by always using the Welch’s t test, which accommodates both unequal and equal variances.
Assessing the ANOVA
In this section, we present the basic concepts underlying the analysis of variance (ANOVA), which compares the means of three or more groups. We also describe some of the more popular post-hoc tests used to follow a statistically significant ANOVA. Finally, we show you how to run commands to execute an ANOVA and post-hoc tests in R, and interpret the output.
Grasping how the ANOVA works
As described earlier in “Surveying Student t tests,” it is only possible to run a t test on two groups. This is why we demonstrated the t test comparing married NHANES participants (M) to all other marital statuses (OTH). We were testing the null hypothesis M – OTH = 0 because we were only allowed to compare two groups! So when comparing three groups, such as married (M), never married (NM), and all others (OTH), it’s natural to think of pairing up the groups and running three t tests (meaning testing M – NM, then testing M – OTH, then testing NM – OTH). But running an exhaustive set of two-group t tests increases the likelihood of Type I error, which is where you get a statistically significant comparison that is just by chance (for a review, read Chapter 3). And this is just with three groups!
The term one-way ANOVA refers to an ANOVA with only one grouping variable in it. The grouping variable usually has three or more levels because if it has only two, most analysts just do a t test. In an ANOVA, you are testing how spread out the means of the various levels are from each other. It is not unusual for students to be asked to calculate an ANOVA manually in a statistics class, but we skip that here and just describe the result. One result derived from an ANOVA calculation is expressed in a test statistic called the F ratio (designated simply as F). The F is the ratio of how much variability there is between the groups relative to how much variability there is within the groups. If the null hypothesis is true, and no true difference exists between the groups (meaning the average fasting glucose in M = NM = OTH), then the F ratio should be close to 1. Also, F’s sampling fluctuations should follow the Fisher F distribution (see Chapter 24), which is actually a family of distribution functions characterized by the following two numbers seen in the ANOVA calculation:
- The numerator degrees of freedom: This number is often designated as
 or
or  , which is one less than the number of groups.
, which is one less than the number of groups. - The denominator degrees of freedom: This number is designated as
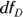 or
or 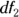 , which is the total number of observations minus the number of groups.
, which is the total number of observations minus the number of groups.
The p value can be calculated from the values of F, 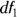 , and
, and 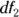 , and the software performs this calculation for you. If the p value from the ANOVA is statistically significant — less than 0.05 or your chosen α level — then you can conclude that the group means are not all equal and you can reject the null hypothesis. Technically, what that means is that at least one mean was so far away from another mean that it made the F test result come out far away from 1, causing the p value to be statistically significant.
, and the software performs this calculation for you. If the p value from the ANOVA is statistically significant — less than 0.05 or your chosen α level — then you can conclude that the group means are not all equal and you can reject the null hypothesis. Technically, what that means is that at least one mean was so far away from another mean that it made the F test result come out far away from 1, causing the p value to be statistically significant.
Picking through post-hoc tests
Suppose that the ANOVA is not statistically significant (meaning F was larger than 0.05). It means that there is no point in doing any t tests, because all the means are close to each other. But if the ANOVA is statistically significant, we are left with the question: Which group means are higher or lower than others? Answering that question requires us to do post-hoc tests, which are t tests done after an ANOVA (post hoc is Latin for “after this”).
Although using post-hoc tests can be helpful, controlling Type I error is not that easy in reality. There can be issues with the data that may make you not trust the results of your post-hoc tests, such having too many levels to the group you are testing in your ANOVA, or having one or more of the levels with very few participants (so the results are unstable). Still, if you have a statistically significant ANOVA, you should do post-hoc t tests, just so you know the answer to the question stated earlier.
- The Bonferroni adjustment uses this calculation to determine the new, lower alpha: α/N, where N is the number of groups. As you can tell, the Bonferroni adjustment is easy to do manually! In the case of our three marital groups (M, NM, and OTH), our adjusted Bonferroni α would be 0.05/3, which is 0.016. This means that for a post-hoc t test of average fasting glucose between two of the three marital groups, the p value would not be interpreted as significant unless the it was less than 0.016 (which is a tougher criterion than only having to be less than 0.05). Even though the Bonferroni adjustment is easy to do by hand, because most analysts use statistical packages when doing these calculations, it is not used very often in practice.
- Tukey’s HSD (“honestly” significant difference) test adjusts α in a different way than Bonferroni. It is intended to be used when there are equally-sized groups in each level of the variable (also called balanced groups).
- The Tukey-Kramer test is a generalization of the original Tukey’s HSD test to designed to handle different-sized (also called unbalanced) groups. Since Tukey-Kramer also handles balanced groups, in R statistical software, only the Tukey-Kramer test is available, and not Tukey’s HSD test (as demonstrated later in this chapter in the section “Executing and interpreting post-hoc t tests”).
- Scheffe’s test compares all pairs of groups, but also lets you bundle certain groups together if doing so makes physical sense. For example, if you have two treatment groups and a control group (such as Drug A, Drug B, and Control), you may want to determine whether either drug is different from the control. In other words, you may want to test Drug A and Drug B as one group against the control group, in which case you use Scheffe’s test. Scheffe’s test is the safest to use if you are worried your analysis may be suffering from Type I error because it is the most conservative. On the other hand, it is less powerful than the other tests, meaning it will miss a real difference in your data more often than the other tests.
Running an ANOVA
Running a one-way ANOVA in R is similar to running an independent t test (see the earlier section “Executing a t test”). However, in this case, we save the results as an object, and then run R code on that object to get the output of our results.
Let’s turn back to the NHANES data. First, we need to prepare our grouping variable, which is the three-level variable MARITAL (where 1 = married, 2 = never married, and 3 = all over marital statuses). Next, we identify our dependent variable, which is our fasting glucose variable called LBXGLU. Finally, we employ the aov command to run the ANOVA in R, and save the results in an object called GLUCOSE_aov. We use the following code: GLUCOSE_aov <- aov(LBXGLU ~ as.factor(MARITAL), data = NHANES). (The reason we have to use the as.factor command on the MARITAL variable is to make R handle it as an ordinal variable in the calculation, not a numeric one.) Next, we can get our output by running a summary command on this object using this code: summary(GLUCOSE_aov).
Interpreting the output of an ANOVA
We describe the R output here, but output from other statistical packages will have similar information. The output begins with the variance table (or simply the ANOVA table). You can tell it is a table because it looks like it has a column with no heading followed by columns with the following headings: Df (for df), Sum Sq (for the sum of squares), Mean Sq (mean square), F value (value of F statistic), and Pr(>F) (p value for the F test). You may recall that in order for an ANOVA test to be statistically significant at α = 0.05, the p value on the F must be < 0.05. It is easy to identify that F = 12.59 on the output because it is labeled F value. But the p value on the F is labeled Pr(>F), and that’s not very obvious. As you saw before, the p value is in scientific notation, but resolves to 0.00000353, which is < 0.05, so it is statistically significant.
Executing and interpreting post-hoc t tests
In the previous example, the ANOVA was statistically significant, so it qualifies for post-hoc pairwise t tests. Now that we are at this step, we need to select which adjustment to use. We already have an idea of what would happen if we used the Bonferroni adjustment. We’d have to run t tests like we did before, only this time we’d have to use the three-level MARITAL variable and run three t tests: One with M and NM, a second with M and OTH, and a third with M and OTH. For each p value we got, we would have to compare it to the adjusted Bonferroni α of 0.016 instead of 0.05. By evaluating each p value, you can determine which pairs of groups are statistically significantly different using the Bonferroni adjustment.
But Bonferroni is not commonly used in statistical software. In R, the most common post-hoc adjustments employed are Tukey-Kramer (using the TukeyHSD command) and Scheffe (using the ScheffeTest command from the package DescTools). The reason why the Tukey HSD is not available in R is that the Tukey-Kramer can handle both balanced and unbalanced groups. In the case of marital statuses and fasting glucose levels in NHANES, the Tukey-Kramer is probably the most appropriate test because we do not need the special features of the Scheffe test. However, we explain the output anyway so that you can understand how to interpret it.
To run the Tukey-Kramer test in R, we use the following code: TukeyHSD(GLUCOSE_aov, conf.level=.95). Notice that the code refers to the ANOVA object we made previously called GLUCOSE_aov. The Tukey-Kramer output begins by restating the test, and the contents of the ANOVA object GLUCOSE_aov.
Next is a table (also known as a matrix) with five columns. The first column does not have a heading, but indicates which levels of MARITAL are being compared in each row (for example, 2-1 means that 1 = M is being compared to 2 = NM). The column diff indicates the mean difference between the groups being compared, with lwr and upr referring to the lower and upper 95 percent confidence limits of this difference, respectively. (R is using the 95 percent confidence limits because we specified conf.level = .95 in our code.) Finally, in the last column labeled p adj is the p value for each test. As you can see by the output, using the Tukey-Kramer test and α = 0.05, M and NM are statistically significantly different (p = 0.0000102), and OTH and M are statistically significantly different (p = 0.0030753), but NM and OTH are not statistically significantly different (p = 0.1101964).
In a real scenario, after completing your post-hoc test, you would stop here and interpret your findings. But because we want to explain the Scheffe test, we can take an opportunity compare what we find when we run that one, too. Let’s start by loading the DescTools package using the R code library(DescTools) (Chapter 4 explains how to use packages in R). Next, let’s try the Scheffe test by using the following code on our existing ANOVA object: ScheffeTest(GLUCOSE_aov).
The Scheffe test output is arranged in a similar matrix, but also includes R’s significance codes. This time, according to R’s coding system, M and NM are statistically significantly different at p < 0.001, and M and OTH are statistically significantly different at p < 0.01. Although the actual numbers are slightly different, the interpretation is the same as what you saw using the Tukey-Kramer test.
Running nonparametric tests
As a reminder, the Wilcoxon Sum-of-Ranks test is the nonparametric alternative to the t test, which you can use if your data do not follow a normal distribution. Like with the t test, you can run a Wilcoxon Sum-of-Ranks test in R with options that gives you results if you are doing a paired t test. But to simply repeat the independent t test we did earlier comparing mean fasting glucose in married NHANES participants compared to all other marital statuses, you would run this code: wilcox.test(NHANES$LBXGLU ~ NHANES$MARRIED).
The Kruskal-Wallis test is a nonparametric ANOVA alternative. Like the ANOVA, you can use the Kruskal-Wallis to test whether the mean fasting glucose is equal in the three-level marital status variable MARITAL. The R code for the Kruskal-Wallis test is different from the ANOVA code because it does not require you to produce an object for the summary statistics. The following code prints the results to the output: kruskal.test(LBXGLU ~ MARITAL, data = NHANES).
Nonparametric tests don’t compare group means or test for a nonzero mean difference. Rather, they compare group medians, or they deal with ranking the order of variables and analyze those ranks. Because it this, the output from R and other programs will likely focus on reporting the p value of the test.
Estimating the Sample Size You Need for Comparing Averages
There are several ways to estimate the sample size you need in order to be able to detect if there is a significant result on a t test or an ANOVA. (Check out Chapter 3 for a refresher on the concepts of power and sample size.)
Using formulas for manual calculation
Chapter 25 provides a set of formulas that let you estimate how many participants you need for several kinds of t tests and ANOVAs. As with all sample-size calculations, you need to be prepared to specify two parameters: the effect size of importance, which is the smallest between-group difference that’s worth knowing about, and the amount of random variability in your data, expressed as the within-group SD. If you plug these values into the formulas in Chapter 25, you can calculate desired sample size.
Software and web pages
All the modern statistical programs covered in Chapter 4 provide power and sample-size calculations for most standard statistical tests. As described in Chapter 4, G*Power is menu-driven, and can be used for sample size calculations for many tests, including t tests and ANOVAs. If you are using G*Power, to estimate sample size for t tests, choose t tests from the test family drop-down menu, and for ANOVA, choose F tests. Then, from the statistical test drop-down menu, choose the test you plan to use and set type of power analysis to “A priori: Compute required sample size – given α, power, and effect size.” Then enter the parameters and click determine to calculate the sample size.
 Such comparisons are generally handled by the famous unpaired or “independent sample” Student t test (usually just called the t test) that we describe later in the section “
Such comparisons are generally handled by the famous unpaired or “independent sample” Student t test (usually just called the t test) that we describe later in the section “ We opted not to clutter this chapter with pages of mathematical formulas for the following tests because based on our own experience, we believe you’ll probably never have to do one of these tests by hand. If you really want to see the formulas, we recommend putting the name of the test in quotes in a search engine and looking on the Internet.
We opted not to clutter this chapter with pages of mathematical formulas for the following tests because based on our own experience, we believe you’ll probably never have to do one of these tests by hand. If you really want to see the formulas, we recommend putting the name of the test in quotes in a search engine and looking on the Internet. The general rule is that N groups can be paired up in
The general rule is that N groups can be paired up in  different ways, so in a study with six groups, you’d have
different ways, so in a study with six groups, you’d have 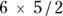 , or 15 two-group comparisons, which is way too many.
, or 15 two-group comparisons, which is way too many.