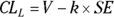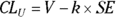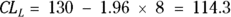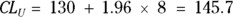Having Confidence in Your Results

Defining confidence intervals

Informally, a confidence interval indicates a range (or interval) of numerical values that’s likely to encompass the true value. More formally, the CI around your sample statistic is calculated in such a way that it has a specified likelihood of including or containing the value of the corresponding population parameter.

The SE is usually written after a sample mean with a ± (read “plus or minus”) symbol followed by the number representing the SE. As an example, you may express a mean and SE blood glucose level measurement from a sample of adult diabetics as 120 ± 3 mg/dL. By contrast, the CI is written as a pair of numbers — known as confidence limits (CLs) — separated by a dash. The CI for the sample mean and SE blood glucose could be expressed like this: 114 – 126 mg/dL. Notice that 120 mg/dL — the mean — falls in the middle of the CI. Also, note that the lower confidence limit (LCL) is 114 mg/dL, and the upper confidence limit (UCL) is 126 mg/dL. Instead of LCL and UCL, sometimes abbreviations are used, and are written with a subscript L or U (as in 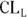or ) indicating the lower and upper confidence limits, respectively.

Although SEs and CIs are both used as indicators of the precision of a numerical quantity, they differ in what they are intending to describe (the sample or the population):

• A SE indicates how much your observed sample statistic may fluctuate if the same study is repeated a large number of times, so the SE intends to describe the sample.
• A CI indicates the range that’s likely to contain the true population parameter, so the CI intends to describe the population.

If you want to have a more precise estimate of your population parameter from your sample statistic, it’s best if the SEs are small and the CIs narrow. One important property of both CIs and SEs is that how big they are varies inversely with the square root of the sample size. For example, if you were to blow up your sample size — let’s pretend to quadruple it — it would cut the size of the SE and the width of the CI in half! This square root law is one of the most widely applicable rules in all of statistics, and is the reason why you often hear researchers trying to find ways to increase the sample size in their studies. In practice, a reasonable sample size is reached based on budget and historical studies, because including the whole population is usually not possible (or necessary).

Understanding and interpreting confidence levels

The probability that the CI encompasses the true value of the population parameter is called the confidence level of the CI. You can calculate a CI for any confidence level, but the most commonly seen value is 95 percent. Whenever you report a CI, you must state the confidence level. As an example, let’s restate our CI from the analysis of mean blood glucose levels in a sample of adult diabetics to express that we used the 95 percent confidence level: 95 percent CI = 114 – 126 mg/dL.

In general, higher confidence levels correspond to wider confidence intervals (so you can have greater confidence that the interval encompasses the true value), and lower confidence level intervals are narrower. As an example, a 90 percent CI for the same data is a smaller range (115–125 mg/dL) and the 99 percent CI is a larger range (112–128 mg/dL).

Although a 99 percent CI may be attractive, it can be hard to achieve in practice because an exponentially larger sample is needed (as described earlier in this section). Also, the wide range it provides can be relatively unhelpful. While dropping to a 90 percent CI would reduce the range and sample size needed, having only 90 percent confidence that the true value is in the range is also not very helpful. This may be why there seems to be an industry standard to use the 95 percent confidence level when calculating and reporting CIs.

The confidence level is sometimes abbreviated CL, just like the confidence limit, which can be confusing. Fortunately, the distinction is usually clear from the context in which CL appears. When it’s not clear, we spell out what CL stands for.

Taking sides with confidence intervals

As demonstrated in the simulation described in the sidebar “Feel Confident: Don’t Live on an Island!”, 95 percent CIs contain the true population value 95 percent of the time, and fail to contain the true value the other 5 percent of the time. Usually, 95 percent confidence limits are calculated to be balanced, so that the 5 percent failures are split evenly. This means that the true population parameter is actually less than the lower confidence limit 2.5 percent of the time, and it is actually greater than the upper confidence limit 2.5 percent of the time. This is called a two-sided, balanced CI.

In some situations, you may want all the failures to be on one side. In other words, you want a one-sided confidence limit. Cars that run on gasoline may have a declaration by their manufacturer that they go an average distance of at least 40 miles per gallon (mpg). If you were to test this by keeping track of distance traveled and gas usage on a sample of car trips, you may only be concerned if the average was below the lower confidence limit, but not care if it was above the upper confidence limit. This makes the boundary on one side infinite (which would really save you money on gas!). For example, from the results of your study, you could have an observed value of 45 mpg, with a one-sided confidence interval that goes from 42 mpg to plus infinity mpg!

In biostatistics, it is traditional to always use two-way CIs rather than one-way CIs, as these are seen as most conservative.

Before you begin: Formulas for confidence limits in large samples

Most of the methods we describe in the following sections are based on the assumption that your sample statistic has a sampling distribution that’s approximately normal (Chapter 3 covers sampling distributions). There are strong theoretical reasons to assume a normal or nearly normal sampling distribution if you draw a large enough samples.

For any normally distributed sample statistic, the lower and upper confidence limits can be calculated from the observed value of the statistic (V) and standard error (SE) of the statistic:

As you can see, CI calculations include a k x SE component, which is both added to and subtracted from the estimate to get the limits. This component is called the margin of error (ME).

Confidence limits computed this way are often referred to as normal-based, asymptotic, or central-limit-theorem (CLT) confidence limits. The value of k in the formulas depends on the desired confidence level and can be obtained from a table of critical values for the normal distribution. Table 10-1 lists the k values for some commonly used confidence levels.

For the most commonly used confidence level, 95 percent, k is 1.96, or approximately 2. This leads to the very simple approximation that 95 percent upper confidence limit is about two SEs above the value, and the lower confidence limit is about two SEs below the value.

The confidence interval around a mean

Suppose that you enroll a sample of 25 adult diabetics (N = 25) as participants in a study, and find that they have an average fasting blood glucose level of 130 mg/dL with a standard deviation (SD) of ±40 mg/dL. What is the 95 percent confidence interval around that 130 mg/dL estimated mean?

To calculate the confidence limits around a mean using the formulas in the preceding section, you first calculate the SE, which in this case is the standard error of the mean (SEM). The formula for the SEM is 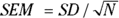, where SD is the SD of the sample values, and N is the number of values included in the calculation. For the fasting blood glucose study sample, where your SD was 40 mg/dL and your sample size was 25, the SEM is 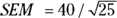, which is equal to 40/5, or 8 mg/dL.

Using k = 1.96 for a 95 percent confidence level (from Table 10-1), the sample mean of 130 mg/dL, and the SD you just calculated of 8 mg/dL, you can compute the lower and upper confidence limits around the mean using these formulas:

On the basis of your calculations, you would report your result this way: mean glucose = 130 mg/dL (95 percent CI = 114 – 116 mg/dL).

Please note that you should not report numbers to more decimal places than their precision warrants. In this example, the digits after the decimal point are practically meaningless, so the numbers are rounded off.

A version of the formula in the preceding section is designed to be utilized with smaller samples, and uses k values derived from a table of critical values of the Student t distribution. To calculate CIs this way, you need to know the number of degrees of freedom (df). For a mean value, the df is always equal to N – 1, so in our case, df = 25 – 1 = 24. Using a Student t table (see Chapter 24), you can find that the Student-based k value for a 95 percent confidence level and 24 degrees of freedom is equal to 2.06, which is a little bit larger than the normal-based k value of 1.96. Using this k value instead of 1.96, you can calculate the 95 percent confidence limits as 113.52 mg/dL and 146.48 mg/dL, which happen to round off to the same whole numbers as the normal-based confidence limits. Generally, you don’t have to use these more-complicated Student-based k values unless your N is quite small (say, less than 25).

The confidence interval around a proportion

If you were to conduct a study by enrolling and measuring a sample of 100 adult patients with diabetes, and you found that 70 of them had their diabetes under control, you’d estimate that 70 percent of the population of adult diabetics has their diabetes under control. What is the 95 percent CI around that 70 percent estimate?

There are multiple approximate formulas for CIs around an observed proportion, which are also called binomial CIs. Let’s start by unpacking the simplest method for calculating binomial CIs, which is based on approximating the binomial distribution using a normal distribution (see Chapter 25). The N is the denominator of the proportion, and you should only use this method when N is large (meaning at least 50). You should also only use this method if the proportion estimate is not very close to 0 or 1. A good rule of thumb is the proportion estimate should be between 0.2 and 0.8.

Using this method, you first calculate the SE of the proportion using this formula: 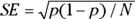where p stands for proportion. Next, you use the normal-based formulas in the earlier section “Before you begin: Formulas for confidence limits in large samples” to calculate the ME and the confidence limits.

Using the numbers from the sample of 100 adult diabetics (of whom 70 have their diabetes under control), you have 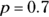and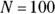. Using those numbers, the SE for the proportion is 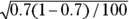or 0.046. From Table 10-1, k is 1.96 for 95 percent confidence limits. So for the confidence limits, 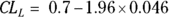and 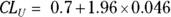. If you calculate these out, you get a 95 percent CI of 0.61 to 0.79 (around the original estimate of 0.7). To express these fractions as percentages, you report your result this way: “The percentage of adult diabetics in the sample whose diabetes was under control was 70 percent (95 percent CI = 61 – 79 percent).”

The confidence interval around an event count or rate

Suppose that you learned that at a large hospital, there were 36 incidents of patients having a serious fall resulting in injury in the last three months. If that’s the only incident report data you have to go on, then your best estimate of the monthly serious fall rate is simply the observed count (N), divided by the length of time (T) during which the N counts were observed: 36/3, or 12.0 serious falls per month. What is the 95 percent CI around that estimate?

There are many approximate formulas for the CIs around an observed event count or rate, which is also called a Poisson CI. The simplest method to calculate a Poisson CI is based on approximating the Poisson distribution by a normal distribution (see Chapter 24). It should be used only when N is large (at least 50). You first calculate the SE of the event rate using this formula: . Next, you use the normal-based formulas in the earlier section “Before you begin: Formulas for confidence limits in large samples” to calculate the lower and upper confidence limits.

Using the numbers from hospital falls example, and 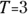, so the SE for the event rate is , which is the same as the square root of 2, which is 1.41. According to Table 10-1, k is 1.96 for 95 percent CLs. So CL_L = 12.0 – 1.96 × 1.41 and CL_U = 12.0 + 1.96 × 1.41, which works out to 95 percent confidence limits of 9.24 and 14.76. You report your result this way: “The serious fall rate was 12.0 (95 percent CI = 9.24 – 14.76) per month.”

To calculate the CI around the event count itself, you estimate the SE of the count N as 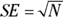, then calculate the CI around the observed count using the formulas in the earlier section “Before you begin: Formulas for confidence limits in large samples.” So the SE of the 36 observed serious falls in a three-month period is simply 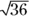, which equals 6.0. So for the confidence limits, we have 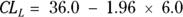and CL_U = 36.0 + 1.96 × 6.0. In this case, the ME is 11.76, which works out to a 95 percent CI of 24.2 to 47.8 serious falls in the three-month period.

Many other approximate formulas for CIs around observed event counts and rates are available, most of which are more reliable when your N is small. These formulas are too complicated to attempt by hand, but fortunately, many statistical packages can do these calculations for you. Your best bet is to get the name of the formula, and then look in the documentation for the statistical software you’re using to see if it supports a command for that particular CI formula.